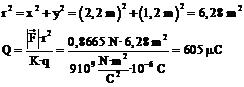|
|
Prácticas de Electricidad SIMULACIÓN DE PROBLEMAS ELECTROSTÁTICOS |
|
|
|
Créditos del material utilizado:
|
|
||
Índice
6.1 Analogía de un campo vectorial con la
velocidad de un fluido
6.2 Representación matemática de un
campo vectorial
6.3 Campo eléctrico
como fuerza eléctrica por unidad de carga
8 Nuevo
enfoque asociado al campo eléctrico
1 Introducción
Una de las dificultades asociadas al estudio de los campos eléctricos es la imposibilidad de ver realmente las líneas de fuerza ni las cargas eléctricas que los crean.
En la práctica 2, se obtuvieron experimentalmente las líneas de campo eléctrico y las líneas equipotenciales de una configuración electrostática. En la presente práctica, se van a obtener resultados equivalentes mediante la simulación de campos eléctricos y gráficos con ordenador.
Por una parte, las grandes posibilidades de representación gráfica con ordenador y la facilidad para cambiar parámetros permiten comprender más fácilmente los problemas. Por otra parte, la simulación utiliza una representación simplificada que desprecia efectos que a veces pueden afectan al sistema (interferencias, variación de parámetros con la temperatura, contactos deficientes, pequeñas fugas de carga, polarización de materiales, etc.). También se elimina el contacto real con el sistema físico que se quiere estudiar, por lo que es necesario compaginar simulación y experimentación.
Las herramientas de simulación se emplean profusamente en el ámbito industrial y de investigación. Permiten el desarrollo de elementos de forma más eficiente pues reducen el número de prototipos que se deben construir y permiten obtener datos en donde la medida real en un prototipo sería muy difícil o incluso imposible.
En la práctica profesional, un buen técnico debe adoptar una actitud crítica con los resultados obtenidos antes de darlos por válidos y deberá construir algún prototipo para verificar la solución final. Esto se debe a que las herramientas de simulación pueden generar resultados erróneos por:
· una modelización deficiente del problema (no considerar algunos efectos que influyen considerablemente al sistema o introducir erróneamente los datos del sistema);
· inestabilidades numéricas (los algoritmos y modelos matemáticos empleados dejan de funcionar correctamente en algunas circunstancias). La resolución de algunos problemas electromagnéticos puede requerir gran precisión de cálculo para obtener soluciones correctas.
Durante la sesión de prácticas únicamente se realizarán los apartados marcados con el símbolo @¤, para no alargarla excesivamente. El resto de apartados que aparecen en este guión se han incluido como ejercicios para hacer en casa que pueden ayudar a afianzar los conceptos vistos en clase. La práctica se puede consultar en Internet en la dirección:
www.unizar.es/icee04/electricidad.htm o www.unizar.es/icee04 (y pulsar el último enlace)
2 Objetivos:
ü
Afianzar los conceptos de
campo eléctrico 
y potencial
eléctrico V.
ü Comprender la equivalencia de la representación de líneas de campo eléctrico, líneas equipotenciales y vectores de campo.
ü
Experimentar con el campo y el potencial
eléctrico V que crean distintas configuraciones de cargas.
ü Observar el principio de superposición a través de un pequeño juego. Comprobar que en la mayoría de casos, sólo afectan significativamente las cargas más próximas porque las interacciones entre cargas puntuales disminuyen con 1/r2.
ü Afianzar el concepto de flujo eléctrico y practicar con su cálculo. Comprobar la ley de Gauss en el vacío y aplicarla para detectar el valor o la posición de las cargas.
ü Estudiar el fenómeno del apantallamiento y de las cargas inducidas en conductores.
3 Conocimientos requeridos
El
estudiante debe manejar con soltura la geometría, vectores,
integración y debe estar familiarizado con el vector intensidad de campo
eléctrico , líneas de fuerza de un campo eléctrico, el
potencial eléctrico puntual V y superficies equipotenciales. Debe
conocer el concepto de flujo eléctrico y debe saber aplicar la ley de
Gauss. También son convenientes nociones básicas de manejo del
ordenador e internet. Se recomienda traer calculadora para
realizar la práctica.
4 Repaso de conceptos[1]
En este apartado opcional se
pueden revisar conceptos como la suma y el producto escalar de vectores y el
concepto de fuerzas conservativas.
4.1 Ejercicios preparatorios.
i.
Pulse sobre el enlace “Suma
de vectores” de la barra de navegación izquierda. Pinchar
sobre un punto del recuadro gris y sin soltar, arrastrar para dibujar un vector
. Repetir el proceso para dibujar el segundo vector 
. Observar que los vectores se pueden desplazar en el plano,
pero no se pueden rotar, alargar o encoger[2].
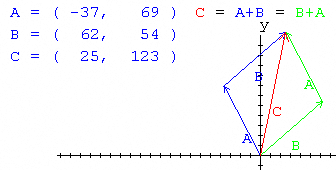
ii. Pulse sobre el enlace “Producto escalar” de la barra de navegación izquierda. Calcular para la situación inicial el ángulo entre los dos vectores.
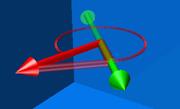
iii. Pulse sobre el enlace “Producto escalar 3D” de la barra de navegación izquierda. Con las teclas de dirección ß y à puede variar el ángulo entre los vectores.
|
El punto de
vista se puede cambiar arrastrando el ratón con el botón
izquierdo pulsando (si además mantenemos pulsado El producto escalar se puede considerar el producto de la longitud del vector verde por la proyección del vector rojo sobre el verde
|
|
5 Ley de Coulomb
En este apartado, se revisarán la Ley de Coulomb como interacción a distancia entre pares de cargas.
|
i. Pulse sobre el enlace “Ley de Coulomb” de la barra de navegación izquierda. Con las teclas de dirección ßáâà puede variar la posición de la carga de prueba. El punto de vista se puede cambiar pulsando y arrastrando el ratón a la vez. Constatar que la fuerza de Coulomb tiene la dirección de la recta que une las dos cargas y es de repulsión para cargas del mismo tipo. Comprobar a ojo que al disminuir la distancia a la mitad, el vector fuerza sobre la carga pequeña aumenta aproximadamente cuatro veces. |
|
ii.
@¤
Pulse sobre el enlace “Calcula la
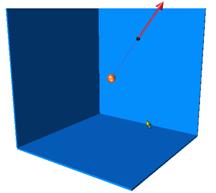
carga” de la barra de navegación izquierda. Disponemos de una
partícula cargada fija (en negro) en el centro del sistema.
|
Podemos mover una pequeña carga de 1 mC (en rojo) pinchando sobre ella y arrastrándola. El vector representa la fuerza que experimenta dicha partícula y en la esquina inferior izquierda se muestra la posición en metros y la fuerza en newtons sobre la partícula móvil. Calcular el valor de la carga negra situada en el centro.
|
|
iv. Pulse sobre el enlace “Ejercicio de superposición” de la barra de navegación izquierda. Vamos a estudiar un sistema formado por dos cargas fijas y una carga de prueba móvil (en la parte inferior del recuadro aparece su posición en metros y la fuerza que experimenta en newtons). Puede observar separadamente la fuerza debida a la primera carga, a la segunda o a ambas cuando actúan simultáneamente sobre la carga de prueba.
@¤
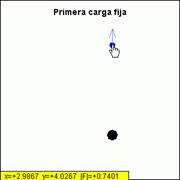
Observe separadamente la fuerza debida a la
primera carga, a la segunda o a ambas cuando actúan
simultáneamente sobre la carga de prueba. Responda a las siguientes
cuestiones relativas al sistema con las dos cargas:
a)
Determine la fuerza neta
sobre la carga de prueba cuando está en el punto inicial (
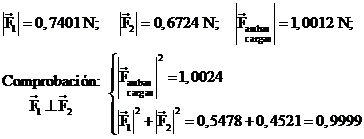
b)
Obtenga la fuerza neta sobre
la carga de prueba cuando se sitúa a mitad de camino entre las cargas
fijas -punto (
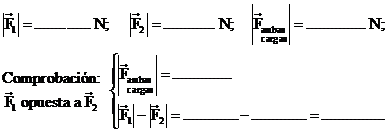
c) ¿Hay punto(s) donde la fuerza total sobre la carga de prueba sea nula? Si es así, anote las coordenadas de algún punto que cumpla dicha condición.
v.
@¤
Pulse sobre el enlace “¿Signo
de las cargas?” de la barra de navegación izquierda. Deducir
el signo de las seis cargas (para ello se pueden mover tanto las cargas negras
como la carga de prueba positiva).
a) ¿Podrías deducir el signo de las cargas únicamente viendo los vectores de campo eléctrico alrededor de las cargas? Pulsa el enlace “Muestra vectores de campo” para tener más pistas.
6 Campo eléctrico
La Ley de
Coulomb explica las interacciones electrostáticas como fuerzas a
distancia. Esto tiene algunas desventajas, como que estas fuerzas a distancia
son instantáneas (según esto, las interacciones
electrostáticas se propagarían a velocidad infinita) y que
dificulta el estudio de problemas con cargas distribuidas en superficies y
volúmenes. El concepto de campo eléctrico permite resolver
problemas que con la ley de Coulomb sería imposible y representa
más fielmente el comportamiento eléctrico de la naturaleza.
El campo eléctrico se representa con líneas de campo o con vectores de campo, pero ambas representaciones son equivalentes. Mientras que las líneas de campo son más adecuadas para dibujarlas a mano, las gráficas por ordenador permiten dibujar los vectores de campo en cada punto, codificando la magnitud del vector por colores (negro indica el máximo valor del campo y azul tenue un campo débil).
6.1
Analogía de un campo vectorial con la velocidad de un fluido
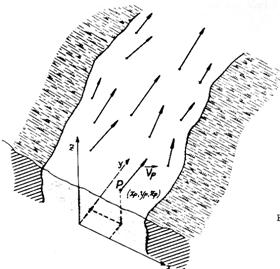
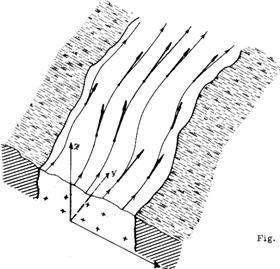
En
cada punto del cauce de un río, la velocidad de una molécula de
agua se puede representar con un vector. Por tanto, a cada punto P del
fluido le corresponde un vector velocidad 
(x, y, z) y podríamos representar la trayectoria de
las partículas con líneas.
6.2
Representación matemática de un campo vectorial
El
campo eléctrico en un punto
representa el ratio entre la fuerza eléctrica que experimentaría
una carga cuando la colocamos en ese punto y el valor de 
Por
tanto, el campo eléctrico se puede
representar matemáticamente como una función que nos devuelve un
vector (tres coordenadas) y cuyos parámetros son las coordenadas del
punto donde queremos conocer su valor. La forma habitual de representar un
vector es por sus componentes:
.
i.
Pulse sobre el enlace “Enfoque
matemático” de la barra de navegación (dentro del
apartado “Campo Eléctrico ”). A continuación nos aparecerá una
animación en la cual podemos introducir la fórmula
matemática[3] de las componentes Ex
y Ey. Cuando pulsamos el botón “actualizar campo
eléctrico”, el ordenador dibuja los vectores de campo
correspondientes a las componentes introducidas[4].
Por defecto, la expresión inicial de las componentes[5] es:
Por ejemplo, si introducimos Ex = 3 y Ey = 4, obtendremos un campo eléctrico uniforme que forma un ángulo:
6.3
Campo eléctrico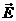como fuerza eléctrica por unidad de carga
Usualmente se utiliza una carga de prueba qp para “medir” o “calcular” el campo eléctrico.
iii.
@¤
Pulse sobre el enlace “Juego con
cargas” de la barra de navegación izquierda. El objetivo de
este pasatiempo es conseguir que una carga móvil describa una
trayectoria sin chocar con una barrera hasta que impacte en
La fuerza total que experimenta la carga
móvil es la suma de las fuerzas que cada carga ejercería
individualmente. Cuando la carga móvil está cerca de otra carga,
el efecto de las demás se puede despreciar porque las fuerzas
culombianas disminuyen muy rápidamente con
b) Describa cómo lo ha hecho. ¿Cuál es el signo de la carga móvil?
vi. Pulse
sobre el enlace “Calcula la carga” de la barra de
navegación izquierda, en el apartado del campo eléctrico. Se dispone de una carga de prueba de 1 nC.
a)
Deducir el valor de la carga
puntual negra a partir del valor de y de la distancia
a la carga (para ver la distancia a la carga negra, pulsar sobre la carga de
prueba roja).
b) ¿Esta carga es debida a un exceso o a un déficit de electrones?
c) Calcular el número de electrones de más o de menos que se precisan para producir el campo observado.
7 Líneas de campo eléctrico
Hay
diversas posibilidades para representar el campo eléctrico creado por
una distribución de cargas. Ya hemos visto cómo hacerlo mediante
los vectores de campo, pero es muy laborioso dibujarlos a mano y
requerirían muchos lápices de colores. En muchas ocasiones se
utilizan las líneas de campo como alternativa, que son más
fáciles de dibujar a mano y que, además, corresponden al concepto
de líneas de fuerza que desarrolló Michael Faraday. En el diagrama de líneas de campo, la
concentración espacial de líneas es utilizada, al menos de forma
cualitativa, para dar una idea del módulo del campo 
. Las flechas indican la
dirección y sentido del campo .
iv.
Pulse sobre el enlace “Vectores
ó Líneas” de la barra de navegación izquierda, en el apartado
de líneas de campo eléctrico.
a)
@¤
Seleccione
b)
Con
c)
Considere
ahora
8 Nuevo enfoque asociado al campo eléctrico[6]
Para aplicar Coulomb necesitamos al menos dos
cargas. En la interpretación de fuerzas a distancia, se necesita siempre una carga para que se manifieste
En la
interpretación de campo, éste existe aunque no haya cargas sobre las que se
manifieste su efecto (por ejemplo, en el vacío). Por tanto, el campo es una propiedad del espacio debida a cargas
eléctricas.
Una posible
interpretación es considerar que las líneas de fuerza del campo se deforman en presencia de cargas, comprimiéndose o
estirándose, generando una “presión eléctrica”
sobre la carga que finalmente experimenta una fuerza. En los vídeos de
esta sección se incluyen algunas animaciones que explican este nuevo enfoque.
Algunas teorías sugieren que las fuerzas eléctricas serían
debidas a algún tipo de intercambio de fotones entre cargas, que se
mueven a la velocidad de la luz (esto explicaría la velocidad de
propagación del campo eléctrico y que las fuerzas disminuyan con
el inverso del cuadrado de la distancia).
9 Cargas distribuidas6
Las animaciones de este apartado muestran
cómo se puede calcular el campo total creado por distribuciones lineales
de carga. El hilo cargado se divide en trozos pequeños, donde cada trozo
crea una contribución al campo eléctrico
y que se representa por los pequeños vectores de
Suma (infinitesimal) de vectores
10 Ley de Gauss
En este apartado se aplicará la Ley de Gauss. En el primer apartado se explorará tridimensionalmente el concepto de integral de superficie y el significado de flujo eléctrico.
i. Pulsar sobre el enlace “Integral de superficie” de la barra de navegación izquierda. Con las teclas de dirección ß áâà puede variar la posición de la carga de prueba.
El punto de vista se puede cambiar
arrastrando el ratón con el botón izquierdo pulsando (si
además mantenemos pulsado
Considere el concepto de integral de superficie, en donde no
sólo importa el módulo del campo eléctrico sino
también la orientación que tiene con la superficie
. Además, el módulo y la
orientación relativa entre y 
pueden cambiar de
un punto a otro de la superficie, tal como ocurre en las animaciones.
a)
@¤
Estime el valor de
En el resto de animaciones, sólo se verá un corte por un plano de la superficie cerrada de Gauss, tal como se hace en clase. Por ejemplo, si utilizamos una superficie esférica, al cortar el sistema por un plano la superficie se representa por un círculo. El estudiante se tiene que imaginar la situación tridimensional, puesto que para aplicar la Ley de Gauss siempre tenemos que considerar una superficie cerrada.
ii.
@¤
Pulse sobre el enlace “Ley de
Gauss” de la barra de navegación izquierda. La
animación muestra en dos dimensiones una parte del mundo tridimensional
(realmente se representa el plano de corte que pasa por las cargas y por el
centro de la superficie gausiana).
La barra
gráfica de la izquierda muestra el flujo del vector intensidad de campo
eléctrico , ΦE, a través de cuatro
superficies gausianas[7].
Observe que la animación
muestra el plano de corte que pasa por las cargas y por el centro de las
superficies gausianas. Tendrá que imaginar que los círculos que
se presentan son esferas y que los cuadrados son cajas. El flujo, en
términos cualitativos, es una medida del número neto de
líneas de campo eléctrico que atraviesan
una superficie dada. Si elige la representación de líneas de
campo , puede observar que cuando el flujo a través de una
superficie gausiana es cero es porque el mismo número de líneas
de campo que entran por
una parte, salen por la otra y por tanto el número neto de líneas
es x + (-x) = 0.
El flujo del campo eléctrico se calcula
matemáticamente con la integral de superficie siguiente :
siendo el campo
eléctrico y el vector
elemento de área o superficie (normal y hacia el exterior de la
superficie, si ésta es cerrada). El ángulo formado por el campo y
la normal a la superficie lo hemos designado por θ.
La Ley de Gauss en el vacío relaciona el flujo a través de una superficie (gausiana) cerrada con la carga neta que hay en su interior (qencerrada):
donde ε0 es una constante denominada permitividad del vacío (8,85 10-12 C2/Nm2).
Comience moviendo la superficie
gausiana de color verde. Fíjese en cómo cambia el valor del flujo
según que la superficie englobe a la carga o la carga quede fuera de
.
Mueva la superficie hacia regiones en que el flujo sea cero. El campo en los puntos de la superficie no es cero y, sin embargo, el flujo es cero. ¿Cómo puede ser así? Si pensamos en términos de líneas de campo (como si de un fluido se tratara, pues el término flujo fue introducido en el estudio de los fluidos) cuando la carga está fuera hay líneas que entran y vuelven a salir. La definición de flujo nos da un signo que es negativo cuando el campo penetra en la superficie y positivo cuando sale. Cuando la carga está dentro de la superficie, sólo hay líneas de campo salientes (si la carga es positiva, entrantes si es negativa) y el flujo neto es distinto de cero. Cuando la simetría de la superficie gausiana está muy alejada de la simetría del campo, es difícil determinar el campo a partir de la Ley de Gauss.
Finalmente pase a estudiar un sistema con dos cargas utilizando la superficie azul. Fíjese en qué sucede cuando la superficie encierra a una sola carga y cuando encierra a las dos.
vii. Pulse
sobre el enlace “Simetría y Ley de Gauss” de la barra
de navegación izquierda.
La Ley de Gauss en el vacío se
cumple siempre: , pero sólo en casos de simetría es
útil, por sí sola, para determinar analíticamente el campo
eléctrico.
Para calcular debemos poderlo
sacar fuera de la integral:
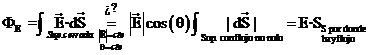
pero esto ocurre
solamente si se mantiene y q constante sobre toda la superficie gausiana. Aquí es donde
interviene y el
ángulo q (que forma con la normal 
) se mantenga constante. En ese caso, la aplicación de
la Ley de Gauss conducirá directamente a la determinación del
campo eléctrico7. En la práctica, esto significa escoger
una superficie gausiana con la misma simetría que el campo.
Considere una esfera alrededor de la carga puntual. La carga de prueba en azul muestra la dirección y sentido del campo eléctrico. Se muestra asimismo un vector, móvil, según la normal a la superficie.
b)
Calcule 
(ponga 
=1) moviendo el
vector normal sobre la superficie y colocando la carga de prueba en tres puntos
diferentes (lea el valor de la intensidad del campo en el recuadro amarillo).
¿Se obtienen los mismos valores? ¿Por qué o por qué
no?
Ponga ahora una caja alrededor de la carga puntual. Asociado a la carga de prueba puede verse el vector campo y el menor ángulo (en grados) formado por el campo con el eje vertical. El vector en rojo (uno para cada lado) muestra el vector normal a la caja.
c)
Calcule (ponga =1) moviendo el
vector normal sobre la superficie y colocando la carga de prueba en tres puntos
diferentes de la superficie superior. ¿Se obtienen los mismos valores?
¿Por qué o por qué no?
d) Teniendo en cuenta su respuesta al apartado anterior, ¿puede valorar si es mejor la esfera o la caja como superficie gausiana que permita una determinación sencilla del flujo?
Pasemos a otra configuración de carga. Ponga una esfera alrededor de un plano cargado (suponga que los círculos grises constituyen alambres que se extienden hasta el infinito, hacia dentro y hacia fuera del plano de la pantalla, para crear un plano cargado del cual sólo ve su sección transversal).
e)
¿Son
prácticamente constantes los valores de en tres puntos cualesquiera de la superficie gausiana?
f) Explique, entonces, por qué no utilizaría una esfera para esta configuración de carga.
Ponga ahora una caja alrededor del plano cargado.
g)
@¤
¿Son prácticamente constantes
los valores de
en tres puntos
cualesquiera de la parte superior?
h) ¿Y qué ocurre en las superficies laterales (verticales)?
Utilizando una caja para el plano cargado,
se obtiene que es constante para
cada superficie parcial (caras superior, inferior y caras laterales). Esto
significa que puede escribirse:
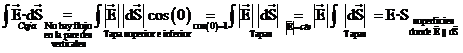
Utilice la Ley de Gauss para demostrar que
el campo eléctrico de un plano cargado con una densidad σ (C/m2)
de carga es: = σ/(2
ε0); para ello deberá utilizar el conocimiento que ya
tiene sobre la simetría del campo; en particular, que es perpendicular
al plano y saliendo de él si la carga es positiva. Puede que le confunda
el 2 en el denominador, pues cuando se habla del campo de un plano
metálico cargado dicho factor no está. Si se da carga a un plano
metálico, se forman dos superficies cargadas (separadas por el espesor
pequeño del metal, en cuyo interior no hay carga y el campo es nulo). El
campo de un plano metálico cargado es: = σ/ε0. Obsérvese que,
en ambos casos (plano cargado o plano metálico cargado), el campo es
homogéneo en cada semiespacio.
viii. Pulse sobre el enlace “Ordene
las cargas ” de la barra de navegación izquierda y “Configuración
@¤
x. Pulse
sobre el enlace “Esferas cargadas I ” de la barra de
navegación izquierda.
¿Cuál es la diferencia entre los campos eléctricos de una esfera cargada en volumen uniformemente (una esfera no conductora) y una esfera metálica cargada? Mueva la carga de prueba para registrar la intensidad de campo eléctrico en función de la distancia al centro de la esfera.
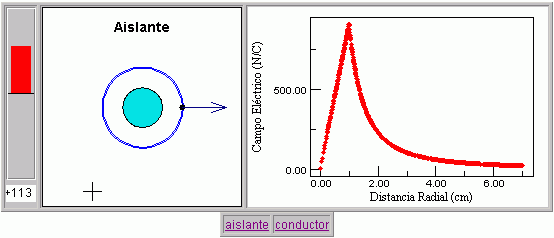
a) Compare los campos eléctricos dentro y fuera de las dos esferas. ¿Qué semejanzas y diferencias encuentra (la carga total de las dos esferas es la misma)?
Pruebe a poner una superficie gausiana grande alrededor de la esfera cargada en volumen. La barra gráfica mide el flujo. Ahora pruebe con una gausiana grande alrededor de la esfera metálica.
b) ¿Por qué son iguales los flujos?
c) ¿Cuánta carga es encerrada por la gausiana en cada caso? ¿Cómo lo sabe?
d) ¿Qué valor cree tendrá el flujo a través de una gausiana interior al metal? ¿Por qué? Compruébelo y explique el resultado.
Pruebe ahora con la misma gausiana pequeña interior a la esfera cargada en volumen.
e) ¿Qué valor de flujo se mide?
f) ¿Qué cantidad de carga está encerrada por esta gausiana pequeña?
g) ¿Cuál es la relación entre la carga encerrada y la carga total de la esfera?
h) ¿Por qué coincide la relación entre el volumen de la esfera pequeña (gausiana) y el volumen de la esfera grande (cargada en volumen) con la relación de cargas obtenida en g)?
i) Utilice la Ley de Gauss para determinar el campo eléctrico en los puntos de la esfera gausiana (punto interior a la distribución de carga). Verifique que el valor obtenido coincide con el mostrado en el gráfico.
xi. Pulse
sobre el enlace “Esferas cargadas II ” de la barra de
navegación izquierda.
@¤
El gráfico muestra el flujo a
través de una esfera que se expande. La esfera cargada se representa por
un círculo sombreado y la superficie gausiana esférica, con un
círculo con doble borde, sin rellenar. Pulse "marcha" para
comenzar la expansión.
a) ¿Cuál corresponde a una esfera con carga únicamente en la superficie?
b) ¿Cuál corresponde a una esfera con carga distribuida a lo largo de su volumen?
c) ¿Podrías calcular en los dos casos la carga total de las esferas?
11 Potencial eléctrico
Se puede asociar
un potencial a cada punto del espacio sin más que elegir un origen (al
que asignamos el valor de referencia 0) y calcular la diferencia de potencial
(d.d.p.) entre ese punto de referencia y cualquier otro. Las unidades del
potencial son las mismas que la d.d.p. (voltio en S.I.).
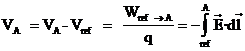
En los programas utilizados en esta práctica, la referencia de potencial se ha tomado en el infinito (es decir, en un punto muy alejado de las cargas).
· Pulse sobre el enlace “Potencial debido a esferas cargadas” de la barra de navegación izquierda.
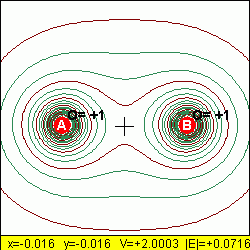
La animación muestra las curvas equipotenciales correspondientes a dos esferas cargadas. Cuando pincha y arrastra el ratón por la animación, se muestran los valores de la intensidad del campo eléctrico y del potencial (posición en metros, potencial eléctrico en voltios y campo eléctrico en newtons/culombio), tal como se puede ver en la imagen anterior. El origen de potenciales se ha puesto en el infinito (muy lejos de las cargas).
a)
Cambie el valor de y V?
b) Estudie ahora la situación con cargas iguales en módulo y signos opuestos. ¿Hay algún punto donde el campo sea cero? ¿Y el potencial?
c)
Cuando
Nota: El potencial eléctrico de una
carga, tomando el origen en el infinito, es un escalar proporcional a la carga
partido por la distancia desde el punto considerado a la carga en
cuestión (V = K q / r ). El potencial eléctrico en el
origen debido a las dos cargas originales es V = K(2Q), ya que r =
·
@¤
Pulse sobre el enlace “Líneas
equipotenciales” de la barra de navegación.
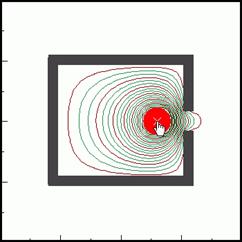
El panel de la izquierda muestra un
diagrama vectorial de un campo electrostático. Las flechas
representan la orientación del campo y el color está asociado a
su intensidad (módulo). El objetivo de este apartado es comprobar la
equivalencia entre la representación de los vectores de campo y las
líneas equipotenciales (que unen puntos con el mismo potencial). Las
líneas equipotenciales se pueden obtener moviendo el lápiz
siempre en dirección perpendicular al campo eléctrico. Cuanto más intenso sea el campo , más juntas estarán las líneas
equipotenciales. Por eso habrá más densidad de líneas
equipotenciales en los puntos con vectores de campo negros, correspondientes a
mayor intensidad de campo eléctrico .
Después de dibujar el diagrama de
líneas equipotenciales correspondiente a la figura de la izquierda,
seleccione cuál de los diagramas propuestos (
· Pulse sobre el enlace “¿Esfera conductora o aislante?” de la barra de navegación izquierda.
@¤
El panel de la izquierda muestra la posición de una carga de prueba y la fuerza que experimenta y en la derecha aparece su potencial. El objetivo de este experimento es determinar el caso que corresponde a la esfera conductora y aislante, y comprobar la expresión obtenida en clase para el potencial de una esfera cargada uniformemente en su volumen.
·
@¤
Pulse sobre el enlace “Calcule el
trabajo” de la barra de navegación izquierda.
La animación muestra un
electrón por una región donde actúa un campo
eléctrico del que se representan algunas líneas equipotenciales.
Ordene de menor a mayor el trabajo efectuado por una fuerza externa para mover al
electrón del punto inicial al final en las Animaciones
12 Apantallamiento
El problema del apantallamiento consiste en
evitar que un campo eléctrico creado en una
cierta región del espacio afecte a otra. Esto tiene gran importancia
práctica, pues el campo eléctrico creado por un circuito puede
afectar a otro cercano, produciendo interferencias electromagnéticas.
Para resolver el apantallamiento, hay que basarse en las propiedades de los conductores en equilibrio electrostático:
o Los conductores son equipotenciales.
o El campo en su interior es cero
En ausencia de
otros objetos cargados, un conductor se descarga al conectarlo a tierra. Pero
si tenemos otros objetos cargados o un campo eléctrico externo, el
objeto no se descarga porque las cargas quedan atraídas. Por eso no se
puede afirmar que un objeto siempre se descargue al conectarse a tierra. Por
ejemplo:
o Un condensador cargado y conectado a tierra sólo por uno de los terminales.
o Carga por inducción electrostática.
o Bola cargada dentro de una jaula de Faraday.
Las técnicas
de apantallamiento se basan en el comportamiento de conductores huecos, ya que
el campo exterior no afecta al interior, tal como comprobaremos en los
siguientes ejercicios.
i.
Pulse sobre el enlace
“Jaula de Faraday” de la barra de navegación izquierda.
Esta animación representa una carga esférica que se puede mover en el interior o en el exterior de una caja metálica conectada a tierra. El borde exterior de la animación también está conectado a tierra. Al mover la carga, puede observar como quedan confinadas las líneas equipotenciales y los vectores de campo.
a) Cuando la esfera cargada está dentro del conductor hueco (jaula de Faraday) ¿podemos decir que un conductor conectado a tierra puede confinar el campo eléctrico de las cargas que hay en su interior? ¿Y si no estuviera conectado a tierra?
b) Cuando la esfera está fuera del conductor hueco, ¿podemos decir que un conductor conectado a tierra puede confinar el campo eléctrico de las cargas que hay en su exterior? ¿Y si no estuviera conectado a tierra?
c) Cuando la esfera está justo en la abertura de la caja metálica ¿queda el campo confinado en el interior, en el exterior o se expande por todo el espacio próximo al agujero?.
|
Observación: A veces, es inevitable que las jaulas de Faraday tengan alguna abertura por donde puede penetrar el campo eléctrico exterior o salir el que se genera en su interior (penetrar o radiar interferencias). Piensa que un circuito, aunque esté dentro de una caja metálica, siempre tendrá que tener un agujero por donde entran los cables y algunas aberturas para permitir su refrigeración. No obstante, habrás podido comprobar que sólo cuando la carga está muy cerca de la abertura no hay confinamiento del campo eléctrico. |
|
ii. Pulse sobre el enlace “Pantalla metálica” de la
barra de navegación izquierda.
El cuadrado rosa
representa un cubo cargado uniformemente (+) en su volumen y se puede mover
horizontalmente. Arrastre el cubo cargado hacia la pantalla metálica
(dibujada en negro) de
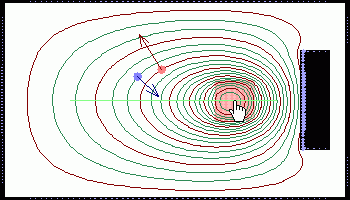
Se han añadido dos cargas de prueba rosa (+) y azul ténue (-), que también se pueden desplazar para medir el campo eléctrico. Las flechas de las cargas representan la fuerza que experimentan (en la carga negativa, el sentido es opuesto al campo eléctrico).
a) Arrastre el cubo cargado horizontalmente hasta hasta el extremo izquierdo o derecho. ¿Por qué se concentran las cargas inducidas preferiblemente cerca del cubo? Ayuda: en la superficie de un conductor |E| = σ/ε0;
b) ¿De dónde provienen las cargas inducidas (azul ténue) que aparecen en las superficies conducoras negras?
c) Ponga cualquiera de las cargas de prueba en el espacio entre el rectángulo conductor negro y el borde exterior conductor (junto al borde de la derecha). ¿se podría decir que esa región está aislada del campo eléctrico que hay a la izquierda por la pantalla (rectángulo conductor negro) de la derecha? Si lo desea, puede comprobarlo viendo la representación del campo eléctrico.
iii. Pulse sobre el enlace “Cubeta de Faraday” de la barra
de navegación izquierda.
|
El proceso de transferencia de carga de un conductor a otro mediante contacto "interno" fue estudiado por Faraday, utilizando como conductor hueco el recipiente metálico donde guardaba el hielo que empleaba en el laboratorio. La animación simula la cubeta de Faraday, un recipiente hueco que tiene una apertura en la parte superior. Un electroscopio conectado a la superficie exterior de la cubeta nos señala la presencia de carga mediante la desviación de su lámina metálica. |
|
a) Comenzamos la "experiencia" pulsando el botón titulado Nuevo.
b) Con el puntero del ratón cogemos una bola que ha sido cargada (positivamente o en color rojo) poniéndola en contacto con un generador electrostático como el de Van de Graaff.
Introducimos la bola por el orificio situado en la parte superior del conductor hueco inicialmente descargado. En el momento en que introducimos la carga, se muestra las cargas inducidas en la superficie interior de la cubeta de signo contrario (negativas o de color azul) y a su vez aparecen en la pared exterior de la cubeta un número igual de cargas positivas (en color rojo). El electroscopio detecta la presencia de carga desviándose ligeramente su lámina metálica indicadora.
c)
Arrastramos la bola con el
puntero del ratón hasta que toque con la pared interior de
d) Pulsamos el botón titulado Otra más. La bola se traslada y se pone en contacto de nuevo con el generador electrostático dispuesta para ser introducida a través del orificio del conductor hueco.
Vamos observando como se va cargando la cubeta, y cómo se desvía un ángulo cada vez mayor la lámina metálica del electroscopio que nos indica la cantidad de carga acumulada.