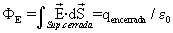Simetría y Ley de Gauss

La Ley de Gauss en el vacío se cumple siempre:
                                                                       ,
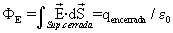aunque sólo en casos de simetría es útil, por sí sola, para determinar analíticamente el campo eléctrico.

Para calcular 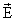 debemos poderlo sacar fuera de la integral:
                          

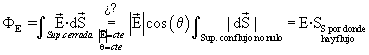
pero esto ocurre solamente si se mantiene |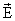|  y q constante sobre toda la superficie gausiana. Aquí es donde interviene la simetría. Si esta simetría es suficientemente acusada como, es posible seleccionar una superficie gausiana en que el módulo del campo eléctrico |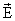|  y el ángulo q (que forma 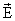 con la normal 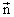) se mantenga constante. En ese caso, la aplicación de la Ley de Gauss conducirá directamente a la determinación del campo eléctrico. En la práctica, esto significa escoger una superficie gausiana con la misma simetría que el campo. La posición está en metros y la intensidad de campo eléctrico está en voltios/metro.  Reinicio.

Considere una esfera alrededor de la carga puntual. La carga de prueba en azul muestra la dirección y sentido del campo eléctrico. Se muestra asimismo un vector, móvil, según la normal a la superficie.

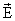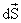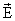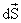1. Calcule •  = || | | cosθ (ponga | 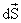| =1) moviendo el vector normal sobre la superficie y colocando la carga de prueba en tres puntos diferentes (lea el valor de la intensidad del campo en el recuadro amarillo). ¿Se obtienen los mismos valores? ¿Por qué o por qué no?

Ponga ahora una caja alrededor de la carga puntual. Asociado a la carga de prueba puede verse el vector campo y el menor ángulo (en grados) formado por el campo con el eje vertical. El vector en rojo (uno para cada lado) muestra el vector normal a la caja.  

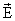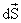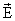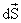2. Calcule •  = || | | cosθ (ponga | 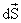| =1) moviendo el vector normal sobre la superficie y colocando la carga de prueba en tres puntos diferentes de la superficie superior. ¿Se obtienen los mismos valores? ¿Por qué o por qué no?
3. Teniendo en cuenta su respuesta al apartado anterior, ¿puede valorar si es mejor la esfera o la caja como superficie gaussiana que permita una determinación sencilla del flujo?

Pasemos a otra configuración de carga.  Ponga una  esfera alrededor de un plano cargado (suponga que los círculos grises constituyen alambres que se extienden hasta el infinito, hacia dentro y hacia fuera del plano de la pantalla, para crear un plano cargado del cual sólo ve su sección transversal).

4. ¿Son prácticamente constantes los valores de E • dS= E dS cosθ en tres puntos cualesquiera de la superficie gaussiana?
5. Explique, entonces, por qué no utilizaría una esfera para esta configuración de carga.

Ponga ahora una  caja alrededor del plano cargado.

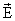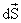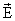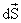6. ¿Son prácticamente constantes los valores de •  = || | | cosθ en tres puntos cualesquiera de la parte superior?
7. ¿Y qué ocurre en las superficies laterales (verticales)?

Utilizando una caja para el plano cargado, se obtiene que 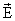•  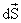= ||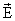 | | 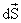cosθ es constante para cada superficie parcial (caras superior, inferior y caras laterales). Esto significa que puede escribirse:
                    

8. Utilice la Ley de Gauss para demostrar que el campo eléctrico de un plano cargado con una densidad σ (C/m²) de carga es: E = σ/(2ε₀); para ello deberá utilizar el conocimiento que ya tiene sobre la simetría del campo; en particular, que es perpendicular al plano y saliendo de él si la carga es positiva. Puede que le confunda el 2 en el denominador, pues cuando se habla del campo de un plano metálico cargado dicho factor no está. Si se da carga a un plano metálico, se forman dos superficies cargadas (separadas por el espesor pequeño del metal, en cuyo interior no hay carga y el campo es nulo). El campo de un plano metálico cargado es: E = σ/ε₀. Obsérvese que, en ambos casos (plano cargado o plano metálico cargado), el campo es homogéneo en cada semiespacio.

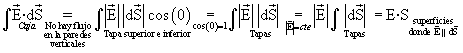
Exploración creada por Anne J. Cox. Script creado por  Wolfgang Christian y modificado por Anne J. Cox. Modificado por Joaquín Mur Amada.
© 2004 Pearson Educación S. A.